Code
library(tidyverse)
library(tidymodels)
library(factoextra)
income_data <- read_csv("../data/adult_income_dataset.csv")Using tidymodels
This document demonstrates how to perform clustering in R using the tidymodels framework. Clustering is an unsupervised learning technique that groups similar data points together based on their inherent characteristics. We will use the adult_income_dataset.csv for this demonstration.
First, we load the necessary libraries and the income dataset.
Rows: 32,561
Columns: 15
$ age <dbl> 39, 50, 38, 53, 28, 37, 49, 52, 31, 42, 37, 30, 23, 3…
$ workclass <chr> "State-gov", "Self-emp-not-inc", "Private", "Private"…
$ fnlwgt <dbl> 77516, 83311, 215646, 234721, 338409, 284582, 160187,…
$ education <chr> "Bachelors", "Bachelors", "HS-grad", "11th", "Bachelo…
$ `education-num` <dbl> 13, 13, 9, 7, 13, 14, 5, 9, 14, 13, 10, 13, 13, 12, 1…
$ `marital-status` <chr> "Never-married", "Married-civ-spouse", "Divorced", "M…
$ occupation <chr> "Adm-clerical", "Exec-managerial", "Handlers-cleaners…
$ relationship <chr> "Not-in-family", "Husband", "Not-in-family", "Husband…
$ race <chr> "White", "White", "White", "Black", "Black", "White",…
$ sex <chr> "Male", "Male", "Male", "Male", "Female", "Female", "…
$ `capital-gain` <dbl> 2174, 0, 0, 0, 0, 0, 0, 0, 14084, 5178, 0, 0, 0, 0, 0…
$ `capital-loss` <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ `hours-per-week` <dbl> 40, 13, 40, 40, 40, 40, 16, 45, 50, 40, 80, 40, 30, 5…
$ `native-country` <chr> "United-States", "United-States", "United-States", "U…
$ income <chr> "<=50K", "<=50K", "<=50K", "<=50K", "<=50K", "<=50K",…# A tibble: 5 × 2
race n
<chr> <int>
1 Amer-Indian-Eskimo 311
2 Asian-Pac-Islander 1039
3 Black 3124
4 Other 271
5 White 27816Rows: 1,000
Columns: 14
$ age <dbl> 19, 51, 57, 23, 47, 23, 40, 32, 37, 27, 26, 42, 40, 3…
$ workclass <chr> "Private", "Private", "State-gov", "Self-emp-inc", "P…
$ fnlwgt <dbl> 47577, 302847, 19520, 214542, 117849, 292023, 280362,…
$ education <chr> "Some-college", "HS-grad", "Doctorate", "Some-college…
$ `education-num` <dbl> 10, 9, 16, 10, 12, 9, 9, 14, 9, 9, 9, 12, 9, 9, 9, 10…
$ `marital-status` <chr> "Never-married", "Married-civ-spouse", "Divorced", "N…
$ occupation <chr> "Transport-moving", "Craft-repair", "Prof-specialty",…
$ relationship <chr> "Not-in-family", "Husband", "Unmarried", "Not-in-fami…
$ sex <chr> "Male", "Male", "Female", "Male", "Male", "Male", "Ma…
$ `capital-gain` <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ `capital-loss` <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ `hours-per-week` <dbl> 50, 54, 50, 50, 44, 45, 35, 40, 40, 40, 40, 40, 84, 6…
$ `native-country` <chr> "United-States", "United-States", "United-States", "U…
$ income <chr> "<=50K", "<=50K", "<=50K", "<=50K", "<=50K", "<=50K",…# Preprocessing using recipes
library(recipes)
income_recipe <- recipe(~ ., data = income_data_clean) %>%
step_dummy(all_nominal_predictors()) %>% # One-hot encode all nominal (categorical) predictors
step_normalize(all_numeric_predictors()) %>% # Normalize all numerical predictors
prep(training = income_data_clean)
income_data_processed <- bake(income_recipe, new_data = income_data_clean)
# Remove any columns that might have resulted in all zeros after one-hot encoding if they were constant
income_data_processed <- income_data_processed[, colSums(income_data_processed) != 0]The Elbow Method is a heuristic used to determine the optimal number of clusters in a dataset. We can visualize the total within-cluster sum of squares as a function of the number of clusters.
K-Means is a popular clustering algorithm. We will use it to group the income data into clusters. The optimal number of clusters can be determined from the Elbow Method plot.
Hierarchical clustering is another common clustering method.
# Calculate the distance matrix
dist_matrix <- dist(income_data_processed, method = "euclidean")
# Perform hierarchical clustering
hclust_model <- hclust(dist_matrix, method = "ward.D2")
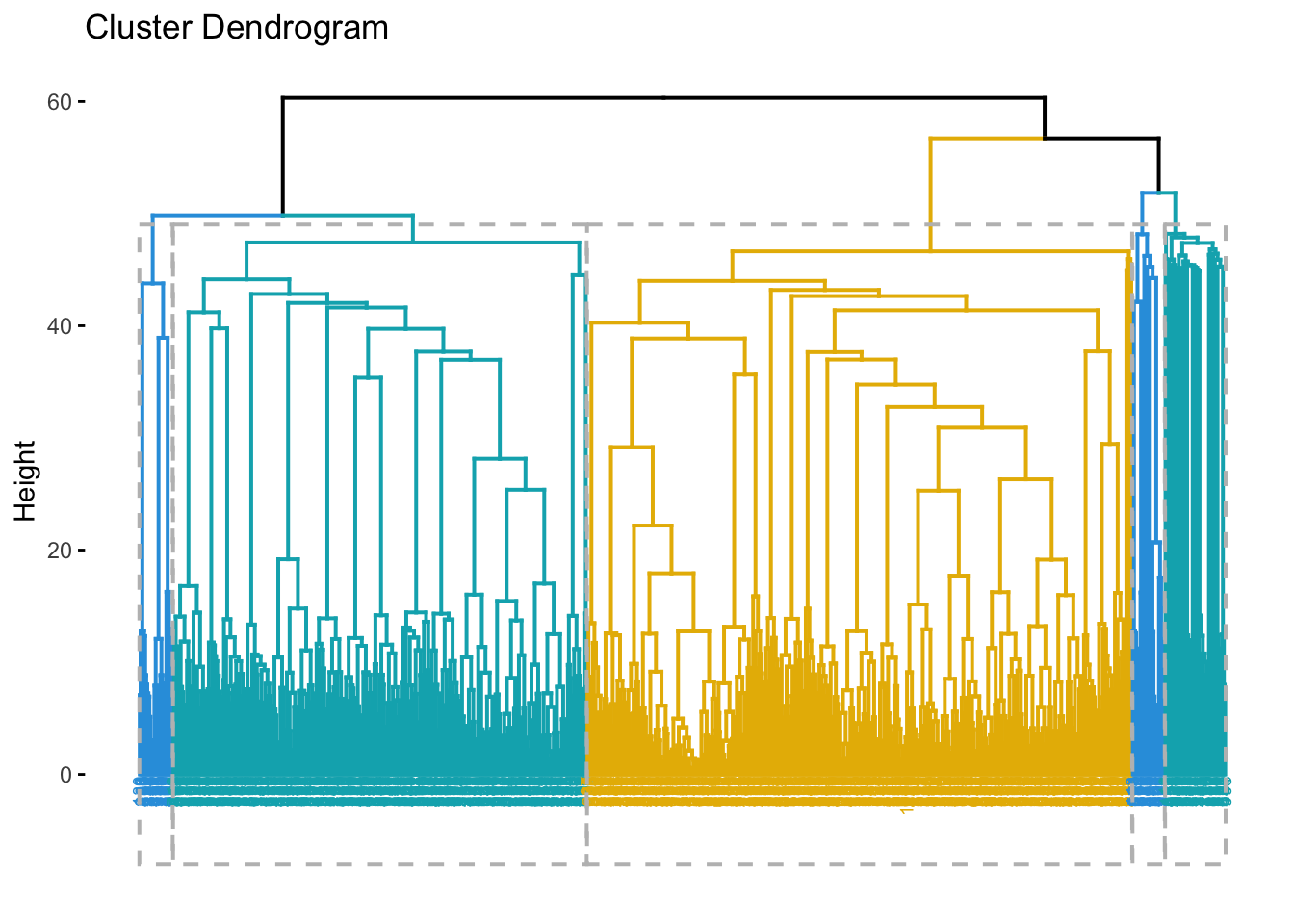
# Visualize the dendrogram
fviz_dend(hclust_model, k = 5,
cex = 0.5, # label size
k_colors = c("#2E9FDF", "#00AFBB", "#E7B800"),
color_labels_by_k = TRUE, # color labels by groups
rect = TRUE # Add rectangle around groups
)
Here’s a comparison of K-Means and Hierarchical Clustering:
|:——————–|:————————————————-|:—————-:————————————-| | Approach | Partitioning (divides data into k clusters) | Agglomerative (bottom-up) or Divisive (top-down) | | Number of Clusters | Requires pre-specification (k) | Does not require pre-specification; dendrogram helps | | Computational Cost | Faster for large datasets | Slower for large datasets (O(n^3) or O(n^2)) | | Cluster Shape | Tends to form spherical clusters | Can discover arbitrarily shaped clusters | | Sensitivity to Outliers | Sensitive to outliers | Less sensitive to outliers | | Interpretability | Easy to interpret | Dendrogram can be complex for large datasets | | Reproducibility | Can vary with initial centroids (unless fixed) | Reproducible |
This document provided a brief overview of clustering in R using tidymodels. We demonstrated both K-Means and Hierarchical clustering on the income dataset.
---
title: "Clustering: Income Data with R"
subtitle: "Using tidymodels"
execute:
warning: false
error: false
format:
html:
toc: true
toc-location: right
code-fold: show
code-tools: true
number-sections: true
code-block-bg: true
code-block-border-left: "#31BAE9"
---
## Introduction
This document demonstrates how to perform clustering in R using the `tidymodels` framework. Clustering is an unsupervised learning technique that groups similar data points together based on their inherent characteristics. We will use the `adult_income_dataset.csv` for this demonstration.
## Load Data
First, we load the necessary libraries and the income dataset.
```{r}
#| label: load-data
#| echo: true
library(tidyverse)
library(tidymodels)
library(factoextra)
income_data <- read_csv("../data/adult_income_dataset.csv")
```
```{r}
glimpse(income_data)
```
```{r}
income_data |> count(race)
```
```{r}
# For simplicity, we'll remove rows with any missing values
income_data_clean <- income_data %>%
select(-race) %>%
na.omit() %>%
sample_n(1000) # Randomly sample 1000 rows
```
```{r}
glimpse(income_data_clean)
```
```{r}
# Preprocessing using recipes
library(recipes)
income_recipe <- recipe(~ ., data = income_data_clean) %>%
step_dummy(all_nominal_predictors()) %>% # One-hot encode all nominal (categorical) predictors
step_normalize(all_numeric_predictors()) %>% # Normalize all numerical predictors
prep(training = income_data_clean)
income_data_processed <- bake(income_recipe, new_data = income_data_clean)
# Remove any columns that might have resulted in all zeros after one-hot encoding if they were constant
income_data_processed <- income_data_processed[, colSums(income_data_processed) != 0]
```
## Elbow Method
The Elbow Method is a heuristic used to determine the optimal number of clusters in a dataset. We can visualize the total within-cluster sum of squares as a function of the number of clusters.
```{r}
#| label: elbow-method
#| echo: true
fviz_nbclust(income_data_processed, kmeans, method = "wss") +
labs(subtitle = "Elbow Method")
```
## K-Means Clustering
K-Means is a popular clustering algorithm. We will use it to group the income data into clusters. The optimal number of clusters can be determined from the Elbow Method plot.
```{r}
#| label: kmeans
#| echo: true
set.seed(123)
kmeans_model <- kmeans(income_data_processed, centers = 5, nstart = 25) # Assuming 2 clusters from Elbow Method
# Visualize the clusters (using first two principal components for visualization)
fviz_cluster(kmeans_model, data = income_data_processed)
```
## Hierarchical Clustering
Hierarchical clustering is another common clustering method.
```{r}
#| label: hclust
#| echo: true
# Calculate the distance matrix
dist_matrix <- dist(income_data_processed, method = "euclidean")
# Perform hierarchical clustering
hclust_model <- hclust(dist_matrix, method = "ward.D2")
# Visualize the dendrogram
fviz_dend(hclust_model, k = 5,
cex = 0.5, # label size
k_colors = c("#2E9FDF", "#00AFBB", "#E7B800"),
color_labels_by_k = TRUE, # color labels by groups
rect = TRUE # Add rectangle around groups
)
```
## Comparison of K-Means and Hierarchical Clustering
Here's a comparison of K-Means and Hierarchical Clustering:
| Feature | K-Means Clustering | Hierarchical Clustering |
|:--------------------|:-------------------------------------------------|:----------------:-------------------------------------|
| **Approach** | Partitioning (divides data into k clusters) | Agglomerative (bottom-up) or Divisive (top-down) |
| **Number of Clusters** | Requires pre-specification (k) | Does not require pre-specification; dendrogram helps |
| **Computational Cost** | Faster for large datasets | Slower for large datasets (O(n^3) or O(n^2)) |
| **Cluster Shape** | Tends to form spherical clusters | Can discover arbitrarily shaped clusters |
| **Sensitivity to Outliers** | Sensitive to outliers | Less sensitive to outliers |
| **Interpretability** | Easy to interpret | Dendrogram can be complex for large datasets |
| **Reproducibility** | Can vary with initial centroids (unless fixed) | Reproducible |
## Conclusion
This document provided a brief overview of clustering in R using `tidymodels`. We demonstrated both K-Means and Hierarchical clustering on the income dataset.